Analysing sparse ecological percent cover data using gllvm

Pekka Korhonen

2025-07-24

This short document showcases how to use the gllvm package to analyse multivariate percent cover data. Namely, we show how to apply the hurdle beta GLLVM (with logistic link), as detailed in Korhonen et al. (2024), to analyse the kelp forest dataset from the Santa Barbara Coastal Long-Term Ecological Research project, available from https://doi.org/10.6073/pasta/0af1a5b0d9dde5b4e5915c0012ccf99c.

A multivariate percent cover dataset often comes in the form of a $n \times m$ matrix $\bf{Y}$, with $n$ being the number of observational units/sites, and $m$ being the number of species of plants, macroalgae, sessile invertebrates, et cetera. The response $y_{ij}$ is then the recorded percentage of the relative area covered by species $j$ on unit/site $i$. Typically such datasets contain considerable proportion of zero observations, as a given obs. unit is often populated by only a small subset of the $m$ species in total. More rarely, it might even be the case that one of the species covers some obs. unit completely.

Hurdle beta GLLVM

Traditionally, beta regression has been used to model responses that take the form of percentages. If $y^*_{ij}$ is in the (open) interval $(0,1)$, and is distributed according to beta distribution, $y^*_{ij} \sim \text{Beta}(\mu_{ij}, \phi_j)$, then it has the following density: $$f_{\text{beta}}(y_{ij}^*; \mu_{ij}, \phi_j) = \frac{\Gamma(\phi_j)}{\Gamma(\mu_{ij}\phi_j)\Gamma(\phi_j-\phi_j\mu_{ij})} (y_{ij}^*)^{\mu_{ij}\phi_j-1}(1-y_{ij}^*)^{\phi_j(1-\mu_{ij}-1)}.$$

The mean parameter $\mu_{ij}$ can be connected to a set of covariates and latent variables through some link function, by the equation $g(\mu_{ij})=\eta_{ij} = \beta_{0j} + \boldsymbol{\beta}_j^\top\bf{x_i} + \boldsymbol{\lambda}_j^\top\bf{u_i}$.

However, such a model is ill-suited for most percent cover datasets, due to the fact that the beta distribution isn’t capable of handling zero (or $100\%$) responses. To make use of the beta regression model in such scenario, one needs to use some transformation in order to ‘push’ the responses away from the boundaries. This procedure might provide reasonable results when the numbers of zeros or ones in the data are relatively low. On the other hand, by transforming the zeros and ones, we might lose some important information.

A more sophisticated way of tackling such issue is by considering a zero-accommodating model, couple of which have been proposed recently. One such model is the hurdle beta model, which models the two (can be extended to three if $100\%$ covers are recorded, see Korhonen et al. (2024)) classes the response $y_{ij}$ can take, i.e., $\{0\}$ and $(0,1)$, by separate processes. Namely, the zeros are assumed to be generated by a Bernoulli process. Conditional on $y_{ij}\in(0,1)$, the response is modeled using the standard beta distribution as presented above. The likelihood function for a response $Y_{ij}$ following the hurdle beta distribution is of the form: $$P(Y_{ij};\mu_{ij}, \mu_{ij}^0, \phi_j) = \begin{cases} 1-\mu_{ij}^0, & Y_{ij} = 0,\\ \mu_{ij}^0 \cdot f_{\text{beta}}(Y_{ij};\mu_{ij},\phi_j), & Y_{ij} \in (0,1). \\ \end{cases}$$ where $g(\mu_{ij}^0) = \eta_{ij}^0 = \beta_{0j}^0 + \bf{x_i}^\top\boldsymbol{\beta}_j^0 + \bf{u_i}^\top\boldsymbol{\lambda}_j^0$ for and $g(\mu_{ij}) = \eta_{ij} = \beta_{0j} + \bf{x_i}^\top\boldsymbol{\beta}_j + \bf{u_i}^\top\boldsymbol{\lambda}_j$ and $g(\cdot)$ can be either probit or logistic link function. Note, that here, the separate linear predictors share the same environmental covariates $\bf{x}_i$ and latent variable scores $\bf{u}_i$, while the coefficients and loadings are allowed to differ.

The gllvm package implements the hurdle beta GLLVM with two different estimation methods available. First, accessed by the argument method="VA" when calling uses a hybrid approach, where the method of variational approximations, or VA, is applied to the Bernoulli-process part of the data (only probit link allowed), while the method of extended variational approximations, see Korhonen et al. (2023), is applied to the beta distributed part. By instead specifying method="EVA", the EVA method is applied to both parts of the likelihood.

Example

In the following, we show how to fit the logistic hurdle beta GLLVM using EVA on the SBC LTER marine macroalgae (i.e., seaweed) percent cover dataset. The data has been collected in 2000-2020 along 44 permanent transect lines along coastal southern California. We will specify a model with two latent variables (for ordination) and will include the rockiness of the seabed and the average number of stripes of giant kelp as environmental covariates in the model.

library(gllvm)

## Loading required package: TMB

## 
## Attaching package: 'gllvm'

## The following object is masked from 'package:stats':
## 
##     simulate

data("kelpforest")
Yabund <- kelpforest$Y
Xenv <- kelpforest$X
SPinfo <- kelpforest$SPinfo

# Data contains both algae and sessile invertebrates
table(SPinfo$GROUP)

## 
##  ALGAE INVERT  PLANT 
##     61     69      2

# Select only the macroalgae:
Yalg <- Yabund[,SPinfo$GROUP=="ALGAE"]

# To demonstrate the models, use only the data from the year 2016:
Yalg <- Yalg[Xenv$YEAR==2016,]
Xenv <- Xenv[Xenv$YEAR==2016,]

# Remove species which have no observations or just one
Yalg <- Yalg[,-which(colSums(Yalg>0)<2)]

# Number of obs. and species:
dim(Yalg)

## [1] 44 42

# Specify the covariates in the linear predictor
Xformulai = ~KELP_FRONDS + PERCENT_ROCKY

After setting up the data, LV design and the covariates, the model is estimated by

fit <- gllvm(Yalg, X=Xenv, formula = Xformulai, family = "betaH", method="EVA", 
             num.lv = 2, link="logit", control=list(reltol=1e-12))

To inspect e.g., the covariate effects, use

fit$params$Xcoef

##            KELP_FRONDS PERCENT_ROCKY
## AU       -4.307914e-02 -4.770042e-03
## BF       -1.853324e+00  7.845708e-02
## BO        3.385302e-01 -6.147463e-02
## BR       -6.183200e-02  2.733598e-02
## BRA       3.260636e-01 -8.164720e-02
## CAL      -1.385751e-01 -2.664296e-02
## CC        9.511590e-02 -1.284133e-03
## CF       -1.328734e-01  9.125119e-03
## CG        3.078440e-02 -3.648815e-02
## CO       -9.359905e-02  1.268354e-02
## COF      -1.011786e-02  7.601417e-04
## CP        2.168726e-02 -7.012546e-02
## CRYP      5.176407e-05 -9.012539e-07
## CYOS      3.569089e-02 -7.728223e-03
## DL        1.015238e-02  1.974069e-02
## DMH       2.028236e-01  8.550216e-03
## DP       -7.015430e-02  7.813939e-03
## DU       -6.720121e-01 -5.758309e-02
## EAH       4.407580e+00 -6.136458e-02
## EC        7.161877e-02  1.579956e-02
## EH        6.005642e-01 -1.139467e-01
## ER       -6.355586e-02 -2.330824e-02
## FB        6.810655e-02  3.410612e-02
## FTHR     -2.401967e-02 -1.913079e-02
## GR        3.016769e-01 -1.434593e-02
## GS       -2.410029e-01 -1.079593e-02
## GYSP     -1.380775e-01  3.815308e-03
## MH        8.944465e-02 -1.296316e-03
## NIE      -1.928211e-02 -6.757693e-03
## PH        1.408930e+00 -2.027203e-01
## PHSE     -3.057175e-01  5.667093e-03
## PL        1.329472e-01 -5.961618e-04
## POLA     -3.064896e-02 -3.633384e-02
## PRSP      1.027000e-05 -1.797908e-07
## R         9.964480e-02  5.434407e-03
## RAT       1.511523e-02  1.733764e-03
## SAFU     -1.899770e+00  1.291657e-02
## SAHO      5.056012e-01 -2.444927e-02
## SAMU     -1.390003e-01 -4.124579e-03
## SCCA     -4.487021e-02  5.600061e-02
## TALE      6.318130e-02 -2.708912e-02
## UV       -8.435144e-01 -4.078454e-02
## H01_AU   -3.748890e-01 -5.090408e-02
## H01_BF   -1.866961e-01 -7.874489e-02
## H01_BO    2.899801e-01 -2.869145e-02
## H01_BR   -9.661864e-02 -4.595573e-03
## H01_BRA   1.603470e-02 -4.446664e-02
## H01_CAL  -2.177546e-01  1.126573e-01
## H01_CC   -1.822890e-01  5.703762e-03
## H01_CF   -4.843186e-02 -1.332073e-02
## H01_CG    8.040600e-02  2.046815e-01
## H01_CO    3.978075e-02 -1.539441e-02
## H01_COF  -2.497741e+00  2.305096e-01
## H01_CP   -8.467667e-02  1.275048e-01
## H01_CRYP -3.409764e-02 -7.639185e-02
## H01_CYOS  1.091321e-01 -1.693727e-02
## H01_DL   -2.191145e-02 -2.713931e-02
## H01_DMH  -1.525665e-01 -1.979245e-02
## H01_DP   -8.902506e-02  1.617001e-02
## H01_DU   -4.162051e-01  2.109371e-01
## H01_EAH  -7.180904e+00  1.875275e-01
## H01_EC    4.734169e-01  1.351968e-01
## H01_EH    1.692431e-01 -4.020182e-02
## H01_ER   -3.849820e-02  4.543815e-02
## H01_FB   -6.363853e-01 -2.517973e-02
## H01_FTHR -4.713358e-01 -4.440901e-02
## H01_GR   -1.897726e-01  2.503153e-01
## H01_GS   -6.117867e-01 -2.390469e-01
## H01_GYSP -3.032503e-02  1.165265e-02
## H01_MH    7.628570e+00 -4.105026e-02
## H01_NIE   3.543694e-01 -7.125865e-02
## H01_PH    4.427246e-01 -8.603485e-02
## H01_PHSE -2.351648e-01 -5.932135e-02
## H01_PL   -1.886402e-02  2.216514e-03
## H01_POLA -1.500098e-01 -2.585375e-02
## H01_PRSP -6.698110e-02 -1.248328e-02
## H01_R    -1.302328e-01  1.389499e-02
## H01_RAT  -1.119953e-01  2.415576e-02
## H01_SAFU -3.568917e+00 -1.324343e-01
## H01_SAHO -2.594287e+00  1.884425e-01
## H01_SAMU -7.460319e-02 -1.506395e-03
## H01_SCCA -9.201648e-02  1.441938e-02
## H01_TALE -5.933011e-01  2.266302e-01
## H01_UV   -7.410063e-01 -1.454605e-02

In the above, the prefix indicates that the coefficient relates to the Bernoulli part of the hurdle model.

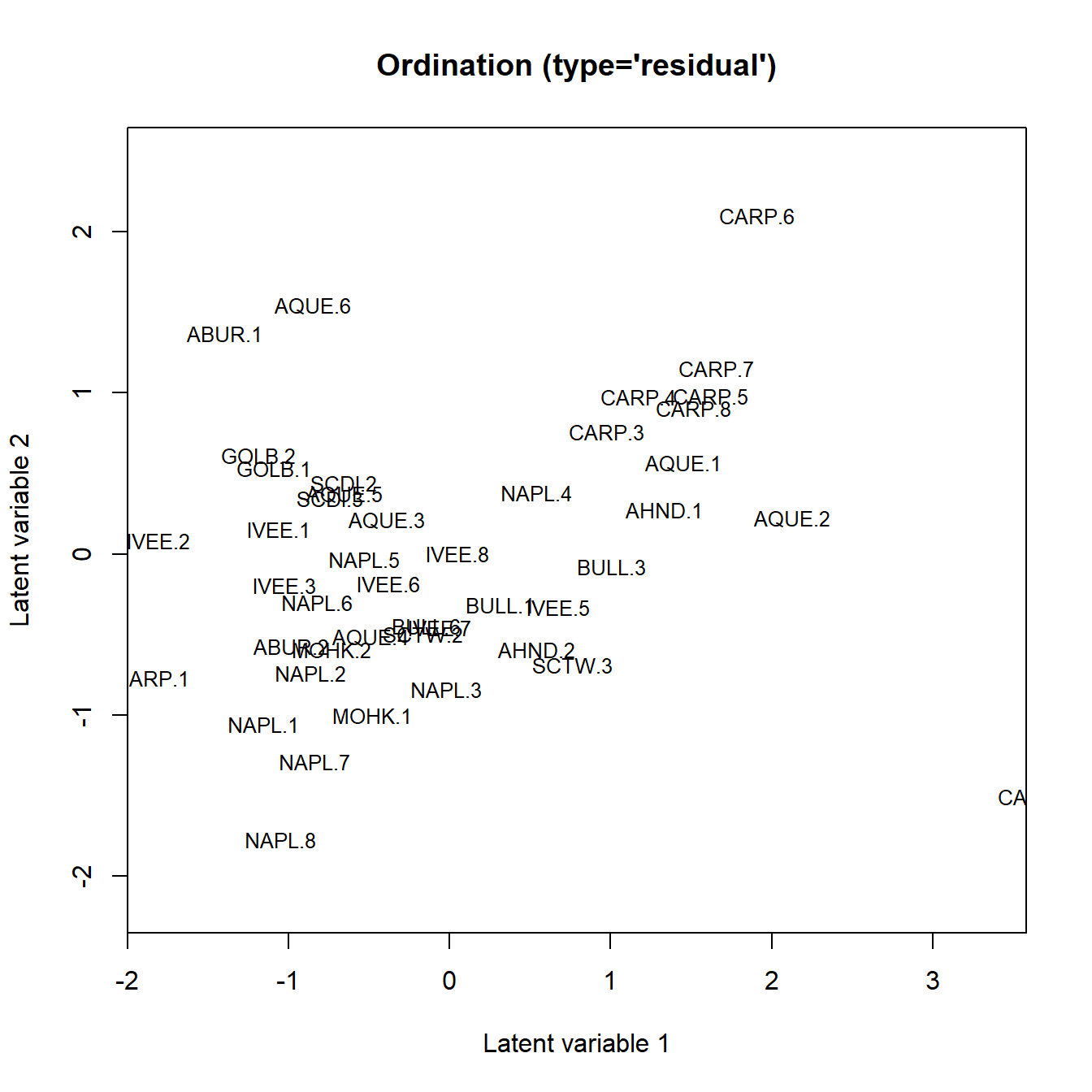
Ordination plot can then be generated as per usual:

ordiplot(fit, jitter = TRUE, s.cex = .8)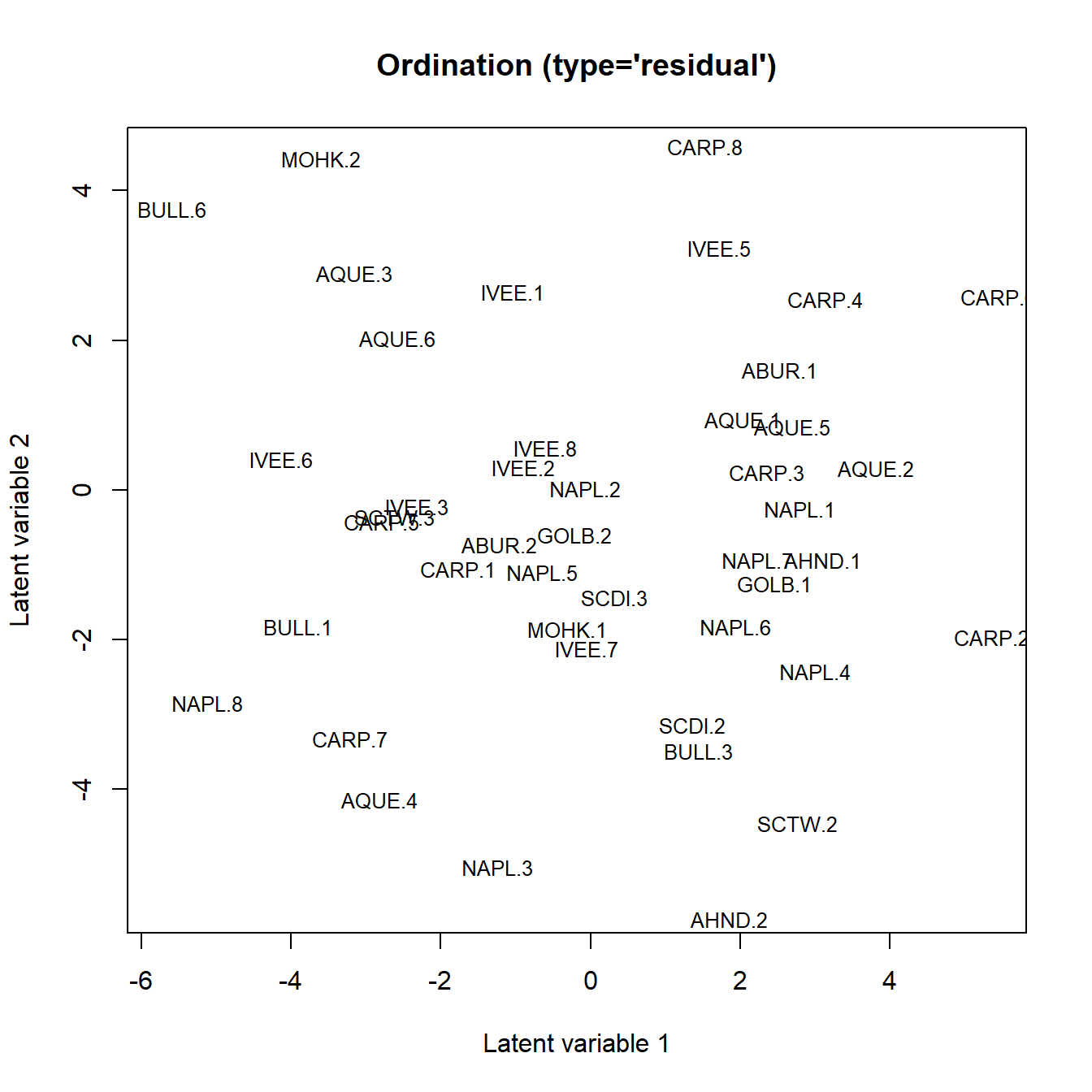

Ordered beta GLLVM

Another solution for modeling percentage cover data in gllvm is to use ordered beta response model. It handles zeros and ones slightly differently compared to hurdle beta model. Instead of assuming that the zeros and ones comes from separate process from the percent cover, the model assumes that there is an underlying process $z_{ij}$ where all observations comes from.

For species $j = 1, . . . , m$, let $z_{ij}$ denote an underlying continuous variable, and define two cutoff parameters $\zeta_{j0} < \zeta_{j1}$ such that $Y_{ij} = 0$ occurs when $z_{ij} < \zeta_{j0}$, $Y_{ij}=1$ occurs when $z_{ij}>\zeta_{j1}$, and $Y_{ij} \in (0,1)$ occurs when $\zeta_{j0} < z_{ij} < \zeta_{j1}$. Conditional on $Y_{ij} \in (0,1)$, the response variable follows a beta distribution. By assuming $z_{ij}$ follows a logistic distribution, then marginalising over $z_{ij}$ we obtain the following distribution for the percent cover responses that characterizes the ordered beta GLLVM,

$$\begin{align} P(Y_{ij};\eta_{ij}, \phi_j) = \begin{cases} \rho^0_{ij}, & if Y_{ij} = 0 ,\\ \left(\rho^1 - \rho^0 \right) \cdot f_{\text{beta}}(Y_{ij}; \mu_{ij}, \phi_j), & if Y_{ij} \in (0,1) ,\\ 1-\rho^1_{ij}, & if Y_{ij} = 1 ,\\ \end{cases} \end{align}$$

Adjusting ordered beta to data without ones

Lets demonstrate the ordered beta response model for the previous example. As the data has no ones:

sum(Yalg ==1)

## [1] 0

We can accommodate the model to better handle data that by fixing the upper cutoff parameters to some large value, for example 20. With gllvm this can be done by setting starting values for the cutoff parameter, ´zetacutoff = c(0, 20)´ and fixing the upper cutoff parameters with ´setMap = list(zeta = factor(c(1:m, rep(NA, m))))´. We assume that the number of species/response variables in the data is saved to object m. There are ´m´ (number of species) lower cutoff parameters $\zeta_{j0}$ we let be freely estimated (that’s indexes ´1:m´ in ´setMap´) and ´m´ upper cutoff parameters $\zeta_{j1}$ that we fix (that’s ´rep(NA, m)´ in ´setMap´).

Setting shape parameter to common across species

Some species are observed only a few times:

colSums(Yalg>0)

##   AU   BF   BO   BR  BRA  CAL   CC   CF   CG   CO  COF   CP CRYP CYOS   DL  DMH 
##   23    3   11    5    2    5   30   13    5   24    5    3    3   33   26    8 
##   DP   DU  EAH   EC   EH   ER   FB FTHR   GR   GS GYSP   MH  NIE   PH PHSE   PL 
##   14    4    3   36    2    6    6    6   11   20    7   36   13    2    5    4 
## POLA PRSP    R  RAT SAFU SAHO SAMU SCCA TALE   UV 
##    6    4   31   17    6    2    7    7    5    6

so there is not much information to estimate the shape parameter of the beta distribution for each species separately. Thus we can also set the shape parameter to be common across species with ´disp.formula = rep(1, m)´. This can be applied for all beta based models in gllvm.

Model fit

Now we are ready to fit the model, we use probit-link function here but logit is also possible similarly to beta hurdle model:

# save the number of species to object m
m <- ncol(Yalg)
fit_ob <- gllvm(Yalg, X=Xenv, formula = Xformulai, family = "orderedBeta", 
    method="EVA", num.lv = 2, link="probit",
    disp.formula = rep(1, m), zetacutoff = c(0, 20),
    setMap = list(zeta = factor(c(1:m, rep(NA, m)))))
fit_ob

## Call: 
## gllvm(y = Yalg, X = Xenv, formula = Xformulai, family = "orderedBeta", 
##     num.lv = 2, method = "EVA", link = "probit", disp.formula = rep(1, 
##         m), setMap = list(zeta = factor(c(1:m, rep(NA, m)))), 
##     zetacutoff = c(0, 20))
## family: 
## [1] "orderedBeta"
## method: 
## [1] "EVA"
## 
## log-likelihood:  265.8511 
## Residual degrees of freedom:  1554 
## AIC:  56.29774 
## AICc:  167.9912 
## BIC:  1679.724

Now if we check the cutoff values we see that the upper bounds are fixed to 20

fit_ob$params$zeta

##          cutoff0 cutoff1
##  [1,] -2.2804694      20
##  [2,] -1.2916900      20
##  [3,] -2.7331047      20
##  [4,] -1.5286385      20
##  [5,] -1.5029773      20
##  [6,] -2.1640885      20
##  [7,] -5.4648841      20
##  [8,] -3.0017473      20
##  [9,] -3.6935325      20
## [10,] -3.4401731      20
## [11,] -5.3251816      20
## [12,] -3.3384571      20
## [13,] -1.5552542      20
## [14,] -3.6606665      20
## [15,] -3.4961040      20
## [16,] -2.4117584      20
## [17,] -2.3677207      20
## [18,] -2.3543442      20
## [19,] -5.6424235      20
## [20,] -4.2557158      20
## [21,] -2.8684617      20
## [22,] -2.7467919      20
## [23,] -0.8132517      20
## [24,] -2.3837258      20
## [25,] -4.5109361      20
## [26,] -3.5332852      20
## [27,] -2.0539203      20
## [28,] -4.3952734      20
## [29,] -3.1997388      20
## [30,] -1.5218883      20
## [31,] -2.3919245      20
## [32,] -1.7326184      20
## [33,] -2.2156611      20
## [34,] -2.1988386      20
## [35,] -4.8337851      20
## [36,] -3.3171903      20
## [37,] -4.6105558      20
## [38,] -8.5070934      20
## [39,] -1.6002892      20
## [40,] -2.3137990      20
## [41,] -3.0606793      20
## [42,] -1.6685450      20

Ordination plot:

ordiplot(fit_ob, jitter = TRUE, s.cex = .8)

References

Korhonen, P., F.K.C. Hui, J. Niku, and S. Taskinen. 2023. “Fast and Universal Estimation of Latent Variable Models Using Extended Variational Approximations.” 33: 26. https://doi.org/10.1007/s11222-022-10189-w.

Korhonen, P., F.K.C. Hui, J. Niku, S. Taskinen, and B. van der Veen. 2024. “A Comparison of Joint Species Distribution Models for Percent Cover Data.” https://doi.org/10.48550/arXiv.2403.11562.